Reconstructing Training Data from Trained Neural Networks

reading papers

どんなものか

• 学習済みのニューラルネットワークモデルから、勾配を用いて学習データを再構成する手法を提案した
  • つまり学習済みモデルから学習データセットを求めた
    
• 

先行研究と比べて

• 多くの研究は学習されたパラメータや表現を分析、可視化することでニューラルネットワークを解読しようとしている
  • 例えばモデルの活性化と強く相関する入力を見つけるなどの手法があり結果は当然訓練データセットと意味的に相関が出てくるが、トレーニングサンプルの正確なデータは見ることができない

技術や手法のポイント

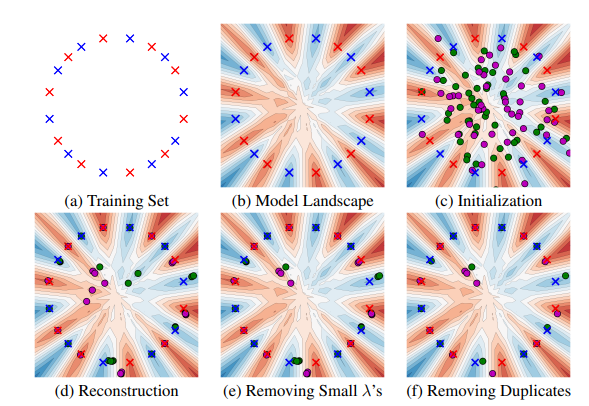
• 訓練データの再構成は初期点したデータ点を、以下の損失を最小化することで学習サンプルに向かってドリフトさせる
  • 学習済みパラメータ $\theta$ （モデルは $\Phi$ とする）とデータセット ${(x_i,y_i)}^n_{i=1}$ が以下の方程式を満たす
  • $\theta = \sum^{n}_{i=1} \lambda_i y_i \nabla \Phi (\theta;x_i)$ (stationarity; 定常性)
  • $\forall i \in [n], y_i \Phi (\theta;x_i) \ge 1$ (primal feasibility; 主制約)
  • $\lambda _1, \cdots , \lambda_n \ge 0$ (dual feasibility; 双対制約)
  • $\forall i \in [n], \lambda_i = 0 ~\text{if}~ y_i \Phi (\theta; x_i) \neq 1$ (complementary slackness; 相補性条件)
  • 上記の定常条件を用いて、損失関数を以下のように定義する

  • $L(x_1, \cdots , x_m , \lambda_1, \cdots , \lambda_m)=

    \theta - \sum^{m}{i=1} \lambda_i y_i \nabla{\theta} \Phi (\theta ; x_i)

    ^2_2$

• 二値分類器がある仮定の下で訓練するとパラメータが定常点に収束することが立証されている。これは学習されたネットワークのパラメータが、学習されたデータセットに対して1組の方程式を満たすことを意味しており学習済みモデル（パラメータ）から逆にデータセットも求まる。

検証方法

• toy datasetsによる実験
  • 
• CIFAR10とMNIST
  • 
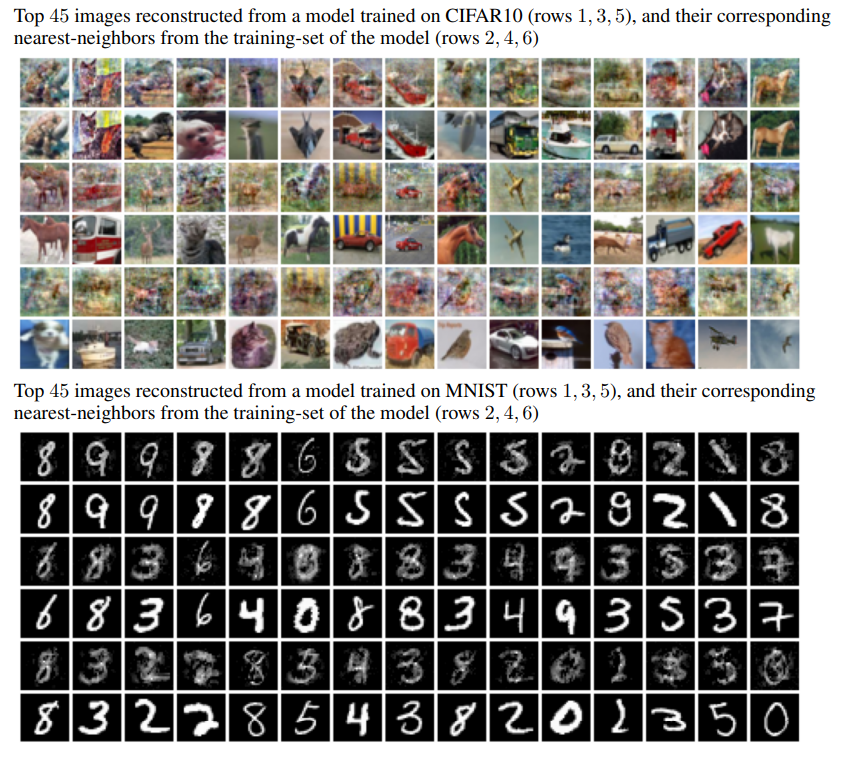
  • 図の1,3,5列目が再構成結果、2,4,6が再構成画像の再近傍（ssimメトリックで算出）の訓練データ
  • CIFAR10では車両と動物、MNISTでは奇数と偶数の二値分類のタスクを考える
  • モデルは入力次元d-1000-1000-1のMLP
• マージンの効果
  • 
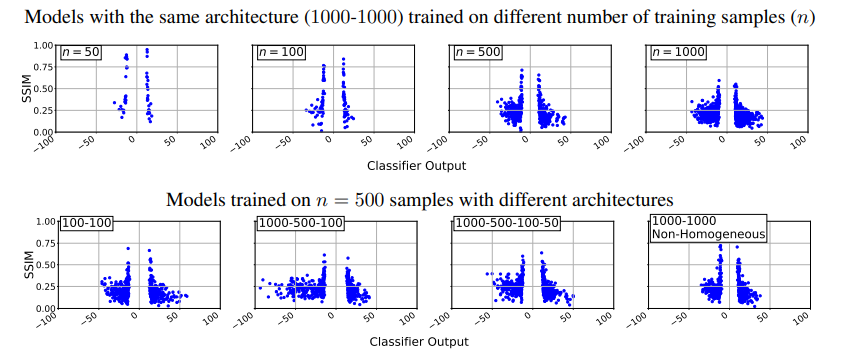
  • データセットのサイズやモデルサイズを変更したときの訓練データのssimメトリックの値
  • データセットはCIFAR10
  • マージン付近の訓練データでssimが高くなっていることから理論的なマージンの有効性が実験的にも有効だと確認された
• 他の訓練データ再構成手法との比較
  • 
  • 定性的に不十分であることが見て取れる

議論

• CNNに対しての理論的な最適化問題の解放はより困難らしい